第十二章、计算理论

奠定了计算科学真正的科学地位

将讨论有关编程语言能力的内在问题

1. 函数及其计算

理解计算机能做什么和不能做什么，以及机器要实现其全部潜能需要哪些特征

  • 函数：可能输入值和可能输出值之间的一种对应关系
  • 对于那些过于复杂以致找不到定义的明确的函数，超过了任何算法的能力范围，成为不可计算的函数

2. 图灵机

用作研究算法处理能力的一种工具

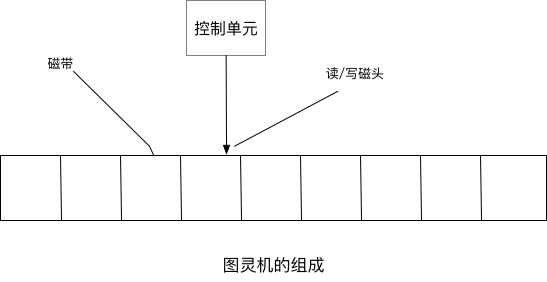
2.1 图灵机的原理

  • 计算开始与一个初始状态，和结果处于停止状态
  • 由控制单元控制执行步骤，左移或右移，来写入数据

2.2 丘奇——图灵论题

图灵机的计算能力囊括了任何算法系统的能力

  • 这个猜想的意义在于，他认识到了计算机器的能力和局限性

3. 通用程序设计语言

如今的许多高级语言知识增强的使用的方便性，对语言的基本功能并没有什么贡献

3.1 Bare Bones语言

从通用设计程序语言中分离出来的需求的最小集合

1. 变量类型

  • 二进制
  • 无需类型转换
1
2
clear X
incr X

2. 赋值语句

1
2
3
4
5
6
# 清空变量为0
clear name
# 增加
incr name
# 减少
decr name

3. 控制语句

  • 只提供一条控制语句
1
2
while name not 0:
  #do something

3.2 用Bare Bones语言编程

  • 提供了一种基本的通用程序设计语言

例子1

  • 赋值操作,将A的值赋值到B
  • 但是会破坏原来A的值
1
2
3
4
clear B
if A not 0:
  incr B
  decr A

例子2

  • 为了不破坏原有的数据，引入了临时变量

  • 通过定义一鞥关键字，来创建一个新的语法copy name1 to name2

1
2
3
4
5
6
7
8
9
clear C
clear B
if A not 0:
  incr C
  decr A
if C not 0:
  incr A
  incr B
  decr C

3.3 Bare Bones的通用性

  • 研究证明，Bare Bones可以用来表示所有的可计算函数的算法
  • 在计算科学理论的研究中常常用到

4. 不可计算函数

4.1 停机问题

一个程序在某些条件开始后，是否能够终止

  • 存在一个单一的、通用的却能够适用于所有情况的算法

例子

  • 如果程序不是以0 开始的，那么程序将不会终止
1
2
while x not 0:
  incr x
  • 可以看出程序能否终止取决于它初始变量的值

自引用技术（self-reference）

思想在与一个对象引用自己

自引用的例子

产生了悖论

  • “这条语句是错的“
  • “所有集合的集合是否包含其自身”

但是

  • 对于这个程序，无论初始值为什么，都会终止
1
2
3
clear x
while x not 0:
  incr x

所以引出以下的定义——自终止（self-terminating）

  • 这是一个属性，要么是，要么不是

如果一个程序中的所有变量都是用程序自身的编码表示来进行初始化的，且这个程序的执行能够导致一个终止的过程

所以

  • 停机问题可以描述为，一个程序是否为自终止的
  • 但是没有一个单一的算法可以确定这个程序是否为自终止的——停机问题超出了计算机的能力
  • 我们只能解决特定问题的下的方案，并没有普遍适用的方法

4.2 停机问题不可解性

  • 利用反证法，先假设存在这样的程序

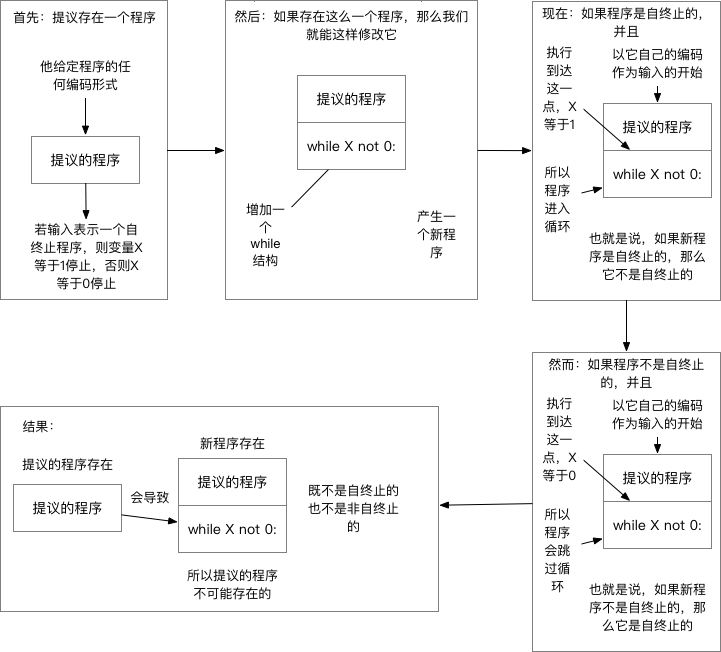
5. 问题的复杂性

不能在合理的时间上解决的问题，在实际观点上来看是无解的

5.1 问题复杂性的度量

问题的复杂性取决于算法的特性

  • 复杂性解释倾向于度量一个算法在表示中所遇到的难度，而不是算法本身的复杂性
  • 复杂性最终相关的是机器在执行一个算法所花费的时间，而不是用来表示解的程序的大小
  • 所以能，又有时间复杂性：定义为一个问题最优解的时间复杂性
  • 但是，寻找一个程序的最优解和确认是程序的最优解本身就是一个难题
  • 所以，使用O(f(n))表示这个问题的复杂性为O(f(n))，但是他还有可能有其他更优的解
  • 时间复杂性和空间复杂性之间的折中

5.2 多项式问题和非多项式问题

如果一个问题是属于$$O(f(n))$$的，其中表达式$$f(n)$$要么是宇哥多项式，要么就是受多项式约束

  • 特征是，具有极长的执行时间

  • P问题是一个判定问题类，这些问题可以用一个确定性算法在多项式时间内判定或解出。如果一个判定性问题的复杂度是该问题的一个实例的规模n的多项式函数，则我们说这种可以在多项式时间内解决的判定性问题属于P类问题。P类问题就是所有复杂度为多项式时间的问题的集合。

  • 确定一个问题是否是多项式问题，在计算机科学中非常重要。已经证明，多项式问题是可解问题，因为除了P问题之外的问题，其时间复杂度都很高，即求解需要大量时间。
  • 理论上有解但其时间复杂度巨大的问题，科学家将其称为难解型问题。对计算机来说，这类问题是不可解的。因此，P问题成了区别问题是否可以被计算机求解的一个重要标志。

5.3 NP问题

NP问题是指可以在多项式时间内被非确定机解决的问题。通常它们的时间复杂度都是指数变量,，如$$O(2^n)$$等

  • 旅行推销员问题（英语：Travelling salesman problem, TSP）是这样一个问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。它是组合优化中的一个NP困难问题，在运筹学和理论计算机科学中非常重要。
  • 在非确定性的算法下和确定性算法下，存在明显的界限，非确定性算法依赖于计算机的创造性（运气？）
  • 目前已经证明所有P问题都是NP问题，那么反之P—NP吗?这就是所谓的“NP问题”。目前P与NP是否等价是一个既没有证实也没有证伪的问题。但是大部分科学家猜想：找一个问题的解很困难，但验证一个解很容易(证比解易)，用公式表示就是P≠NP。
  • 问题较难求解(P)但容易验证(NP)，这与我们的日常生活经验是相符的。

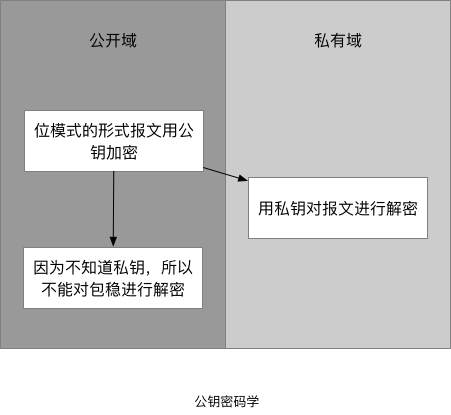
6. 公钥密码学

利用了问题难解易验证的特性

  • 比如寻找某个大整数的因数
  • 在密码学领域里，被用作RSA算法

6.1 模表示法

  • 如果p&q都是素数，m是0到pq的一个整数，那么，对于任意的正整数K，就有$$1 = m^{k(p-1)(q-1)}\% pq$$

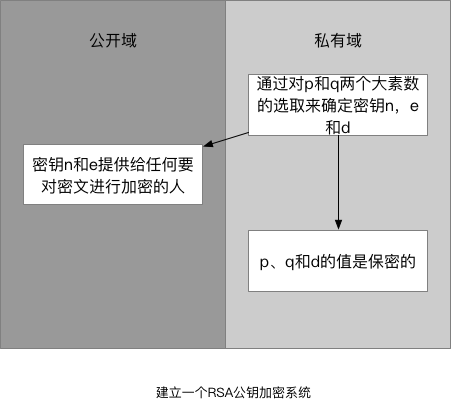
6.2 RSA公钥密码学

  • 两个素数p和q，n = p*q，两个正整数e,d,k，满足

$$
e*d=k(p-1)(q-1)+1
$$

  • 这里选取了5个值，p、q、n、e、d。e、n是加密密钥，d、n是解密密钥，p、q只是用来构建加密系统

加密

  • 位模式（ASCII、Unicode）编码，值小于n（如果大于n，则需要分段）
  • 设报文的值为m(m<n)，则，加密后的报文为$$c=m^e \% n$$

解密

  • 解密的值为：$$c^d\%n$$，余数就是加密前的值
  • 利用了$$1 = m^{k(p-1)(q-1)}\% pq$$

$$
c^d\%n=m^{ed}\%n=m^{k(p-1)(q-1)+1}\%n=mm^{k(p-1)(q-1)}\%n=m*m^{k(p-1)(q-1)}\%pq=m
$$

破解

  • 通过对n进行因式分解，得到p&q，了解到解密的过程中$$c^d\%n$$，像办法得到d，
  • 找出一个k值，使得k(p-1)(q-1)+1能够被e整除（商就是d ），$$k(p-1)(q-1)+1 \div e =d$$
  • 但是在与隐式分解的难度，可能需要好几年才能破解完成

例子(p=7,q=13,n=91,e=5,d=29)

  • 10111 -> 23 -> $$23^e=23^5=6436343$$ -> $$23^5 \% n = 23^5\%91=4$$ -> 100
  • $$4^d=4^{29}=288230376151711744$$ -> $$4^29 \% n = 4^29 \% 91=23$$ -> 10111

最后更新： 2018年07月11日 14:10

原始链接： https://ilifexiao.github.io/2018/06/20/计算机科学概论/第十二章、计算理论/